Бодолт 1.

Хариу: $C_{12}^{6}$.


Бодлогыг $2n\times 2m$ шатрын хөлөг дээр бодолт хийе. Энэ үед байрлуулах хүүгийн тоо $mn$ ба эдгээрийг аль нь ч нэг нүүдлээр нөгөөгөө идэж чадахгүй байхаар байрлуулах боломжийн тоог $f(n, m)$ гэе.

Шатрын хөлөгөө $mn$ ширхэг $2\times 2$ жижиг квадратуудад хуваая. Тэгвэл өгсөн нөхцөл ёсоор аль ч $2\times 2$ дотор хамгийн олондоо нэг хүү байж болно. Тэгвэл дотроо хүүтэй $2\times 2$ квадратууд дараах бүлэгт хуваагдана.

Зүүн дээд буландаа хүүтэй квадратыг 1-р төрлийн квадрат, баруун доод буландаа хүүтэй квадратыг 2-р төрлийн квадрат гэж нэрлэе. 1-төрлийн квадратын дээр болон зүүн талд зөвхөн 1-төрлийн квадрат байж болно. Үүнтэй адилаар 2-төрлийн квадратын дээр болон зүүн талд зөвхөн 2-төрлийн квадрат байж болно. Иймээс 1-төрлийн квадратууд дээрээс болон зүүн тийшээ, 2-төрлийн квадратууд доороос болон баруун тийшээ хэлбэртэй дүрс үүсгэнэ. Энэ 2 дүрсийн хүрээгээр үүсэх муруй нь $2n \times 2m$ шатрын хөлөгийн баруун дээд булан хүртлэх зам болно.

Нөгөө талаас зүүн доороос баруун дээшээ чиглэлтэй зам алхам бүр нь 2 нүднээс тогтох замууд нь 1 ба 2-р төрлийн квадратын хүрээ болж чадна. Иймээс нийт замын тоо $C_{n+m}^m$ байдаг тул манай бодлогын хариу $f(n, m)=C_{n+m}^m$.

Дүгнэх аргачлал: Бодолт-I.

1. Квадратаа $2\times 2$ жижиг квадратуудад хуваах санаа гаргавал 1 оноо.
   


2. $2\times 2$ квадрат хамгийн олондоо 1 хүү байна гэвэл 1 оноо.
   


3. 2 төрлийн квадрат байна гээд тэдгээрийн дээр болон доор, зүүн баруун талыг зөв авч үзэн дүгнэвэл 2 оноо.
   


4. Бүтэн бодолт 7 оноо.
   

Бодолт 2.

Бодлогыг $2n\times 2m$ шатрын хөлөг дээр бодолт хийе. Энэ үед байрлуулах хүүгийн тоо $mn$ ба эдгээрийг аль нь ч нэг нүүдлээр нөгөөгөө идэж чадахгүй байхаар байрлуулах боломжийн тоог $f(n, m)$ гэе. $f(0, m)=1$

Шатрын хөлөгөө $mn$ ширхэг $2\times 2$ жижиг квадратуудад хуваая. Тэгвэл өгсөн нөхцөл ёсоор аль ч $2\times 2$ дотор хамгийн олондоо нэг хүү байж болно. $2\times 2$ жижиг квадратуудын цагаан нүдний аль нэгэнд л хүү байрлаж болох тул $$f(m, n)=f(n-1, m)+f(n, m-1)$$ рекуррент томъёо гарна. Энэ рекуррент томъёог бодох замаар $f(m, n)=C_{m+n}^m$ гэж гаргана.

Дүгнэх аргачлал: Бодолт-II.

1. Квадратаа $2\times 2$ жижиг квадратуудад хуваах санаа гаргавал 1 оноо.
   


2. $2\times 2$ квадрат хамгийн олондоо 1 хүү байна гэвэл 1 оноо.
   


3. Рекуррент харьцаагаа зөв бичвэл 2 оноо.
   


4. Бүтэн бодолт 7 оноо.
   

Бодолт 1.

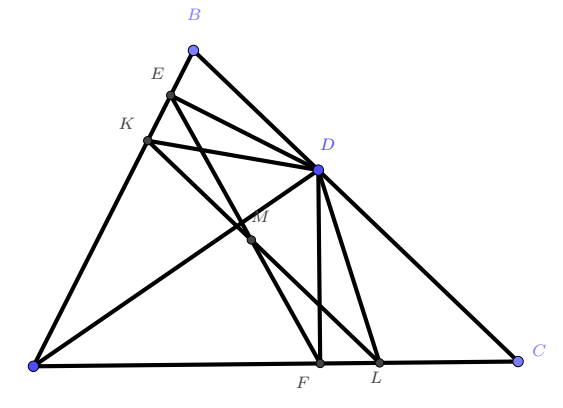
$\angle KED=\angle KMD=90^\circ$ учраас $K, E, D, M$ цэгүүд нэг тойрог дээр оршино.
$\angle LMD=\angle LFD=90^\circ$ учраас $M, D, L, F$ цэгүүд нэг тойрог дээр оршино. Эндээс

\[ \angle BAD=\angle EFD=\angle MFD=\angle MLD=\angle KLD \]
мөрдөж $A, K, D, L$ цэгүүд нэг тойрог дээр оршино. Эндээс

\[ \angle BKD=\angle ALD,~ \angle ADL=\angle AKL=\angle ABC\] болж $\triangle KBD\sim \triangle LDA$ гарна. Төсөөгийн харьцаагаар
$\dfrac{1}{2}=\dfrac{BD}{AD}=\dfrac{BK}{DL}$ болж $DL=2BK$ батлагдана.

Онооны схем

1. "$A, K, D, L$ цэгүүд нэг тойрог дээр оршино'' гэсэн үр дүн, мөн үүнтэй эквивалент үр дүнд 3 оноо,
   


2. "$AOK$, $BDK$ гурвалжнууд төсөөтэй" гэж баталбал 3 оноо,
   


3. Бүтэн бодолт 7 оноо