
ММО-62, I даваа, E (9-10) ангилал
1.
$3^n$ болон $n!$ тоонууд ижил цифрээр эхэлдэг байх хамгийн бага натурал $n$ тоог ол.
Хариу: 6
2.
$f(x) = ax^{2}+bx+c$ квадрат гурван гишүүнтийн хувьд $f(1) = 2$, $f(2) = 6$, $f(6) = 2$ байдаг бол $f(5)$ утгыг ол.
Хариу: 6
3.
$1000 \times 1002 \times 1004 \times \dots \times 2026$ үржвэр хамгийн ихдээ $7$-гийн хэдэн зэрэгтэд хуваагдах вэ?
Хариу: 84
4.
$19\sqrt{3}$ урттай талтай квадрат дотор том жижиг хоёр зөв гурвалжин зурагт үзүүлснээр байрлаж байв. Жижиг зөв гурвалжингийн талын уртыг ол.
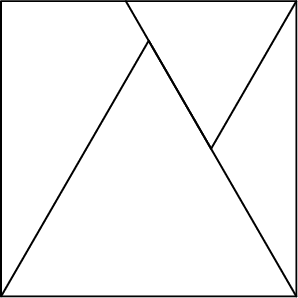

Хариу: 19
5.
${(2n+1)}:{m}$ ба ${(2m+1)}:{n}$ харьцаанууд бүхэл байдаг $m$, $n$ натурал тоонуудын хувьд $mn$ үржвэр хамгийн ихдээ хэд байж болох вэ?
Хариу: 21
6.
$3 \times 3$ хүснэгтийн нүднүүдэд натурал тоонуудыг мөр болон багана болгоны тоонуудын нийлбэр $6$ байхаар хэдэн янзаар бичиж болох вэ?
Хариу: 55
7.
$ABCD$ тэгш өнцөгтийн талууд $AB = 20$ ба $AD = 26$ урттай байв. $CD$ талын дундаж цэгийг $M$ гээд $NM$ хэрчмийн дундаж цэг $A$ байхаар $N$ цэгийг авав. $NBD$ гурвалжны талбайг ол.
Хариу: 650
8.
$a+2b=2$ ба $a^2+2b^2=3$ бол $29a^3 +88 b^3$ нийлбэрийг ол.
Хариу: 148
9.
$\angle ABC = 90^\circ$ тэгш өнцөгт гурвалжинд багтсан тойргийн төвийг $I$ гээд $BI$ шулуун $ABC$ гурвалжныг багтаасан тойргийг дахин $D$ цэгт огтолдог гэе. $I$ цэгийг дайрсан $AC$ талтай параллел шулуун $AB$ талыг $M$ цэгт, $BC$ талыг $N$ цэгт огтолно. $BM = 3$ ба $BN = 4$ бол $BD^{2}$ утгыг ол.
Хариу: 72
10.
Дөрвөн оронтой $\overline{abcd}$ тоо хөрвүүлсэн $\overline{dcba}$ тооноосоо тэгш тоо дахин бага байв. $\overline{abcd}$ тоог ол.
Хариу: 2178
11.
Хоёр ялгаатай анхны тооны нийлбэрт яг гурван янзаар бичигддэг хамгийн бага натурал тоог ол. Энд нэмэгдэхүүний байр сольсныг ижил нийлбэр гэж үзнэ.
Хариу: 24
12.
$F_{1} = F_{2} = 1$ ба $n \ge 3$ үед $F_{n} = F_{n-1}+ F_{n-2}$ байдаг дараалал өгөгдөв. $F_{1000}$ гишүүнийг $991$-д хуваахад гарах үлдэгдлийг ол.
Хариу: 55