1. $\dfrac{2}{3}$, $\dfrac{2}{5}$, $\dfrac{4}{5}$, $\dfrac{2}{7}$, $\dfrac{4}{7}$, $\dfrac{6}{7},\dots$ дараалал өгөгдөв. $\dfrac{2022}{2023}$ тоо энэ дарааллын хэд дэх гишүүн бэ?

Хариу: 511566

2. $S(n)$-ээр $n$ тооны цифрүүдийн нийлбэрийг тэмдэглэе. $n=2022S(n)$ нөхцөлийг хангах хамгийн бага $n$ натурал тоог ол.

Хариу: 54594

3. 59-д хуваахад 1 үлдэгдэл өгдөг, 2022-д хуваахад 59 үлдэгдэл өгдөг хамгийн бага натурал тоог ол.

Хариу: 97115

4. Ямар ч $x$ бодит тооны хувьд $|x-1|+|x-2|+\dots+|x-n|\ge 59$ тэнцэтгэл биш биелдэг байх хамгийн
бага $n$ натурал тоог ол.

Хариу: 16

5. $x$, $y$ бодит тоонууд $x+y+\dfrac{x}{y}=10$ ба $\dfrac{x(x+y)}{y}=20$ системийн шийдүүд бол $x+y$ нийлбэрийн авч болох бүх утгуудын нийлбэрийг ол.

Хариу: 10

6. $ABC$ гурвалжны $AB$ тал дээр $P$ цэгийг $3AP=AB$ байхаар, $BC$ тал дээр $Q$ цэгийг $4BQ=BC$ байхаар, $AC$ тал дээр $R$ цэгийг $5CR=AC$ байхаар тус тус авав. Хэрэв $ABC$ гурвалны талбай $24$-тэй тэнцүү бол $PQR$ гурвалжны талбайг ол.

Хариу: 10

7. Дараах зурганд 5 ширхэг гурвалжин өгөгдөв. Ерөнхий талтай гурвалжнууд нь ялгаатай өнгөтэй байхаар 3 өнгө ашиглан (өнгө бүр ядаж нэг удаа орно) хэчнээн янзаар будаж болох вэ?

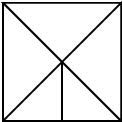
Хариу: 30

8. $\dfrac{1}{x}+\dfrac{1}{2y}+\dfrac{1}{3z}=\dfrac{4}{3}$ тэгшитгэлийн натурал шийдийн тоог ол.

Хариу: 3

9. $f(x)=x^4+3x^3+3x+2$ олон гишүүнтийн язгуурууд $r$, $s$, $t$, $u$ болог.
$$\dfrac{1}{r^2}+\dfrac{1}{s^2}+\dfrac{1}{t^2}+\dfrac{1}{u^2}=\dfrac{n}{m}$$
ба $\dfrac{n}{m}$ нь үл хураагдах бутархай бол $\sqrt{nm}$ тоог ол.

Хариу: 6

10. $ABC$ гурвалжны $\angle ABC=120^\circ$ ба энэ өнцгийн дотоод биссектриссийн суурийг $D$ гэе. Хэрэв $BD=21$, $AB+BC=100$ бол $AB\cdot BC$-г ол.

Хариу: 2100

11. Элементүүдийнх нь нийлбэрийг $12$-д хуваахад $1$ үлдэгдэл өгдөг $\{1,2,3,\dots,12\}$ олонлогийн $3$ элементтэй дэд олонлогийн тоог ол.

Хариу: 18

12. $ABCD$ тэгш өнцөгтийн $AB$ талын дундаж цэгийг $M$ гэе. $BD$ диагонал дээр $\angle MNC=90^\circ$ байх, $B$ цэгээс ялгаатай $N$ цэг авав. $MC$, $NB$ шулуунууд $P$ цэгт огтлолцоно. Хэрэв $AB=4\sqrt{21}$, $BD=24$ бол $NP$ хэрчмийн уртыг ол.

Хариу: 9